先日行われた全国学力テストが新聞に出てたので、やってみました
……数学だけ。
だって、国語は文字が小さすぎて読めなかっただもん。
老眼の兆候か……？
小・中の問題なんか楽勝だよー、と軽くみていました。所詮ヒマ潰しさー、みたいな。
しかし！ 意外と忘れていることも多くて結構難しく、「証明の仕方ってどんなんだっけ？」「円柱：円錐の体積は確か3:1だったような…」などなど、脳みそをフル回転させて定理や数式を搾り出しながらなんとか解く有様でした。
フー、いい脳運動だ
で、問題も解き終わり、答え合わせをしていたのですが、どうしても、ひとつだけ理解できない問題があったんです。
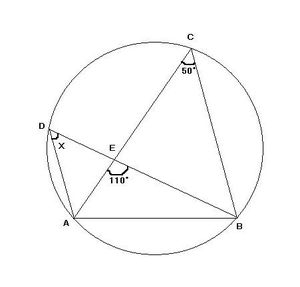このＸ の角度を求めよ、という問題だったのですが、ぜんっぜんわからないんっすよ。
恐らく∠Ｅ110°がヒントなんだろうと当りをつけていろいろやってみるのですが、全く検討がつかないというか、考える術がないというか
結局、答えも見ても正解があるだけで、「どうしてその答えになるのか」が書いてないんです。答えはわかっても、「なぜだ！？」の疑問は膨らむばかりで、最終的に実父に電話しちゃいました。理系だし、わかるかなと思って。
そしたら、こんなメールがパソコンに送られてきたのです。
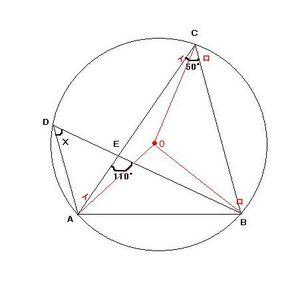添付ファイル：右のイラスト
タイトル：
∠AEB70°はひっかけ
本文：
中心点Ｏに注目すること
△AOCは二等辺三角形なので∠ACO＝∠CAO
同様に、△BOCの場合は∠BCO＝∠CBO
∠AOC＝180－2ｲ
∠BOC＝180－2ﾛ
∠AOB＝360－∠AOC－∠BOC
＝360－(180－2ｲ)－(180－2ﾛ)
＝2(ｲ＋ﾛ)
∠AOB＝2∠ACB
したがって、一定の弦に対する円周角と中心角は1:2の関係にあると言える
この法則を元にすると、同様に∠AOB＝2∠ADBの数式も導き出すことができる（※１）ので、∠ACB＝∠ADBとなり、答えは50°となる
円周角の定理：1つの弧ABに対する円周角は，中心角の半分であり、1つの弧ABに対する円周角は，すべて等しい
以上。
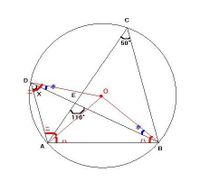※１
∠AOB＋∠AOD＝∠BOD
(180－2ﾊ)＋(180－2ﾆ)＝180－2ﾎ
360－2ﾊ－2ﾆ＝180ー2ﾎ
180－2ﾊ＝2(ﾆ－ﾎ)
！！！！！
まさか∠Ｅの110°は全く無視すべき要素であったとは！！ これが唯一のヒントだと思って、この数字を元に計算して答えを探していくのだと思ったのに
"円周角の定理"とやら、そういわれると習ったような記憶があります。
スカリワスレテタヨ、ワタシ。
わざわざ証明までつけて教えてくれたお父さん先生、とてもわかりやすかったです。ありがとうございました。
今年57歳にもなるのに、未だに数学の公式を覚えてるお父さん。
どんな頭してるのかなと、改めて尊敬したのです。
コメント